The image above was created using AI. More specifically, this was the fourth image generated by Stable Diffusion, when given the prompt “Ice Cream Python Logistic Regression”.

Somewhat recently, I wrote some code for a Colab-assignment from my Applied AI in Python class, which I thought was pretty cool and was a good opportunity to understand the Linear Logistic Regression model.

So to start, we need something to model. This assignment in particular asked us to predict whether a soccer player would get injured based on the player’s age and the number of minutes the player plays.

Creating and Preparing the Data

Below is a very small dataset of 11 players, where each term in the list is a player, the first term of each sublist is the number of minutes played, the second term is player’s age, and the third term is whether or not a player was injured (with 1 meaning injured and 0 meaning not injured):

data = [
[78,32,0],
[34,27,1],
[78,21,1],
[79,28,1],
[75,21,0],
[43,24,1],
[13,29,1],
[17,37,0],
[70,32,0],
[85,23,0],
[63,30,0],
]

We can then convert this data from a python list to a pandas dataframe:

import pandas as pd
df = pd.DataFrame(data, columns = ['average minutes', 'age', 'injured'])

Which allows us to assign column labels: average minutes, age, and injured. A plot of this data:

Now, we can prepare this dataset by converting the dataframe into an actually useable dataset using Numpy and Pandas.dataframe methods:

X = df.iloc[:, :-1]
y = df.iloc[:, -1]
X = np.c_[np.ones((X.shape[0], 1)), X]
y = y[:, np.newaxis]
theta = np.zeros((X.shape[1], 1))

Here, X represents the set of coordinates of each data point in the format [1., x_coordinate, y_coordinate], and y is a set of boolean indicators representing whether a point will be orange or blue in the format [0/1]. For now, theta is just a Numpy array with 0s. For completeness, we print these:

X: [[ 1. 78. 32.]
[ 1. 34. 27.]
[ 1. 78. 21.]
[ 1. 79. 28.]
[ 1. 75. 21.]
[ 1. 43. 24.]
[ 1. 13. 29.]
[ 1. 17. 37.]
[ 1. 70. 32.]
[ 1. 85. 23.]
[ 1. 63. 30.]]
y: [[0]
[1]
[1]
[1]
[0]
[1]
[1]
[0]
[0]
[0]
[0]]
theta: [[0.]
[0.]
[0.]]

Training the Model

To define the model, I used the Gradient Descent Logistic Regression class provided by my instructor:

import numpy as np
from scipy.optimize import fmin_tnc

class LogisticRegressionUsingGD:
def sigmoid(x):
return 1 / (1 + np.exp(-x))
def net_input(theta, x):
return np.dot(x, theta)
def probability(self, theta, x):
return self.sigmoid(self.net_input(theta, x))
def cost_function(self, theta, x, y):
m = x.shape[0]
total_cost = -(1 / m) * np.sum(
y * np.log(self.probability(theta, x)) + (1 - y) * np.log(1 - self.probability(theta, x)))
return total_cost
def gradient(self, theta, x, y):
m = x.shape[0]
return (1 / m) * np.dot(x.T, self.sigmoid(self.net_input(theta, x)) - y)
def fit(self, x, y, theta):
opt_weights = fmin_tnc(func=self.cost_function, x0=theta, fprime=self.gradient, args=(x, y.flatten()))
self.w_ = opt_weights[0]
return self
def predict(self, x):
theta = self.w_[:, np.newaxis]
return self.probability(theta, x)
def accuracy(self, x, actual_classes, probab_threshold=0.5):
predicted_classes = (self.predict(x) >= probab_threshold).astype(int)
predicted_classes = predicted_classes.flatten()
accuracy = np.mean(predicted_classes == actual_classes)
return accuracy * 100

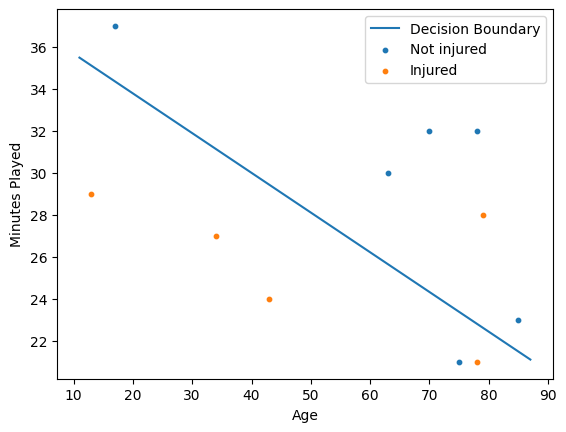
How cool!