The above image was the first image generated by Stable Diffusion when inputted the prompt “Counting Letters in Five-Letter Words”.

As mentioned in my previous blog post, my previous technique to find the optimal starting word in Wordle was highly inefficient. Although it wasn’t completely messy code-wise, the method I employed took way to many calculations to be considered a feasible solution to this dillemma. As a refresher, The algorithm itself was pretty simple: “Direct Intersection” refers to letters that are congruent and are located in congruent positions within a word; comparing the words “apple” and “angle” results in three direct intersections: “a__le”. “Indirect Intersection” to refer to letters that appear in both words, but are not in the same position; comparing the words “intel” and “tenet”, we have indirect intersections for “n”, 2″t”, 2″e”. Notice that despite an e being a direct intersection, it is also an indirect intersection. The algorithm essentially compared every word to every other word by directly checking if a certain letter in a certain place was the same, and if the letter was present in both words. However, this method entailed hundreds of billions of direct comparisons (197,688,192,000 to be exact), which eventually led to program force stops.

So I decided to change up my strategy, counting how many times each letter appeared in each place, then aggregate the information to assign a score to each word. Then, using this score, I could rank words and find the optimal word.

We ended up with the following code:

for letter in Letterchecks:
    for word in words_5:
        for lettercheck in range(0, 4):
            if word[lettercheck] == letter[0]:
                dict[letter] += 1

for letter in sorted(dict, key=dict.get, reverse=True):
    print(letter, dict[letter])

Running this code resulted in:

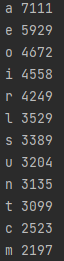
Which demonstrated that the vowels were some of the most common letters in 5-letter words. But this dataset only shows popularity of letters by the ltter itself. A much more useful dataset would be one that counted how many times a certain letter appeared in a certain place, so score weighing would be more precise.

Although it is very spaghetti-like, the following code is a good starting point to count (it is also copy pasteable):

Letterchecks = ["a0","b0","c0","d0","e0","f0","g0","h0","i0","j0","k0","l0","m0","n0","o0","p0","q0","r0","s0","t0","u0","v0","w0","x0","y0","z0","a1","b1","c1","d1","e1","f1","g1","h1","i1","j1","k1","l1","m1","n1","o1","p1","q1","r1","s1","t1","u1","v1","w1","x1","y1","z1","a2","b2","c2","d2","e2","f2","g2","h2","i2","j2","k2","l2","m2","n2","o2","p2","q2","r2","s2","t2","u2","v2","w2","x2","y2","z2","a3","b3","c3","d3","e3","f3","g3","h3","i3","j3","k3","l3","m3","n3","o3","p3","q3","r3","s3","t3","u3","v3","w3","x3","y3","z3","a4","b4","c4","d4","e4","f4","g4","h4","i4","j4","k4","l4","m4","n4","o4","p4","q4","r4","s4","t4","u4","v4","w4","x4","y4","z4"]

This code is a list of every letter with every possible position it could be in (0-4 instead of 1-5, because it makes lists easier to manipulate).

Now using code very similar to my previous strategy of 1-to-1 word comparison, we are able to count how many times each letter appears in each place, in the entire 5-letter dictionary:

f = open("words_alpha.txt")
bigChunkofText = f.read()
words = bigChunkofText.split('\n')
words_5 = []
Letterchecks = ["a0","b0","c0","d0","e0","f0","g0","h0","i0","j0","k0","l0","m0","n0","o0","p0","q0","r0","s0","t0","u0","v0","w0","x0","y0","z0","a1","b1","c1","d1","e1","f1","g1","h1","i1","j1","k1","l1","m1","n1","o1","p1","q1","r1","s1","t1","u1","v1","w1","x1","y1","z1","a2","b2","c2","d2","e2","f2","g2","h2","i2","j2","k2","l2","m2","n2","o2","p2","q2","r2","s2","t2","u2","v2","w2","x2","y2","z2","a3","b3","c3","d3","e3","f3","g3","h3","i3","j3","k3","l3","m3","n3","o3","p3","q3","r3","s3","t3","u3","v3","w3","x3","y3","z3","a4","b4","c4","d4","e4","f4","g4","h4","i4","j4","k4","l4","m4","n4","o4","p4","q4","r4","s4","t4","u4","v4","w4","x4","y4","z4"]

for word in words:
    if len(word)==5:
        words_5.append(word)
dict = {}

for letter in Letterchecks:
    dict[letter] = 0
for letter in Letterchecks:
    for word in words_5:
        for lettercheck in range(0, 5):
            if word[lettercheck] == letter[0] and lettercheck == int(letter[1]):
                dict[letter] +=1
for letter in sorted(dict, key=dict.get, reverse=True):
    print(letter, dict[letter])

Running this code prints the dictionary at the end, resulting in:

Woah! “a” actually isn’t actually the most common letter in a certain position?! Thinking about it a little, it actually kind of makes sense that an “s” at the end would be the most common, since plural forms of nouns end in “s”!

Now, all we need to do is to devise a simple way to combine aggregate scores of each letter in a word, and then find the highest scoring words.